Get this e-book, AutoHotkey Tricks You Ought to Do with Windows!
The Best Free Windows Utility Software Review
"The Free Windows Software I Actually Use"
by Jack Dunning
August 8, 2014
There are many lists of the "Best Free Windows Software" on the Web. Most are merely regurgitations of someone else's list. I'm interested in programs that benefit me everyday, not some clever apps that I'll never use. However, what I find useful may not be the same for you. Everyone uses their computer in a different way. All I can do is tell you what I do.
I love free software,
but the world is drowning in free software. There are so many programs
that
you can pick up at no cost, you'd wonder if anyone ever buys software
anymore. The truth is that in spite of the massive number of
applications available, people only use a few favorites—whether paid or
not. That's why I have to laugh when people tout that the iTunes store
(or any other software delivery platform) has 1.2 million apps. It
makes no difference how many apps are available if they are not the
ones you want.
If I find a truly useful program, I hang onto it. In the beginning I
may load a newly recommended application, but the real test is whether
in the long term
I continue using it. There are many programs that I've
taken for a test drive, but most fall into disuse.
Windows
8.1 Note:
I've used Windows 8.1
on my new laptop
for a while now. I've
slowly converted everything over from my old laptop making the new one
my workhorse. I still have the old laptop in the network just in case I
need to access it. (One of the great things about Google's Chrome Remote Desktop (free) is
that it can remotely access any computer (Windows, Mac, Linux)
including the
Home Premium version of Windows—which cannot be accessed with
Microsoft's own Remote Desktop software).
One interesting
note is that since I've started using Windows 8.1 on a
regular basis, I don't use the Modern user interface or any of its
installed apps at all. It's wasted on me. It may be useful to many
other people, but I find that in my work I have no reason to access the
tablet-like interface. The closest I come is when I need to do a search
( +Q
and the sidebar
with the Everywhere search field pops up).
+Q
and the sidebar
with the Everywhere search field pops up).
Other than the low
value Modern UI, I like Windows 8.1. It's fast and
all of my programs run well on the Windows Desktop. I use my QuickLinks AutoHotkey app (also free to
anyone who wants it, see Figure 1) to replace the missing Windows 8
Start Menu. Even when I eventually upgrade to Windows 9 next year and
the Start Menu returns (supposedly), I will continue to use QuickLinks
as I do now on all my Windows computers.
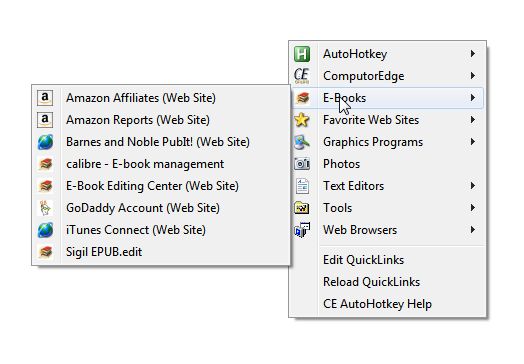
Figure 1. Jack's AutoHotkey QuickLinks app for favorite Web sites and programs in a pop-up menu.
I've installed all of the following free programs on my Windows 8.1 laptop because they are part of my regular routine. (They are already on all my other Windows computers.) Many of these applications have been improved since I first wrote about them (and quite a few more) in Jack's Favorite Free Windows Programs. The two missing from the book are AutoHotkey which is now my number one all-time favorite free software and Foxit PDF Reader, a must-have replacement for the bloated, annoying Adobe Reader. However, AutoHotkey is more like a complete toolbox full of all types of tools (hammers, screwdrivers, saws, etc.) for various uses, while these other programs are individual power tools (drill presses, chain saws, lathes, etc.) for specific types of work. AutoHotkey will never replace these special purpose software packages, but it can certainly enhance them with added features. (The e-book Jack's Favorite Free Windows Programs is available free at ComputorEdge E-Books in both EPUB format for computers and tablets, and MOBI format for Amazon Kindle.)
IrfanView Graphics Viewer
What's notable about my most used free programs is that they either appear pinned to the Windows Taskbar or I've added them to my AutoHotkey QuickLinks. One that I must put near the top of the list of best free programs is the IrfanView graphics viewer (see Figure 2). I use IrfanView on a regular basis and have it pinned to my Taskbar. While I do use other graphics programs, this one is the best for manipulating images. Every week I need to capture, crop and resize images for ComputorEdge. I have found nothing easier or quicker than IrfanView. It has even replaced Windows Snipping Tool for screen capture because it has so many more options and is much easier to use.
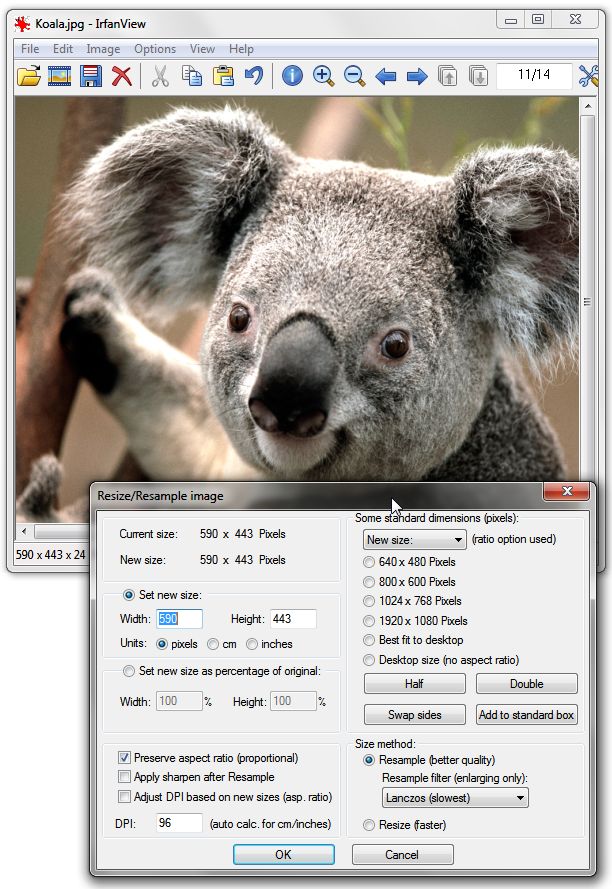
Figure 2. IrfanView is the number one free graphics manipulation tool for features and ease of use.
I can understand how IrfanView may not be at the top of everyone's list. Most people don't need to work with images nearly as much as I do. This is why "best free software" lists vary from person to person.
Windows Paint
I'm forced to admit that I use Windows Paint (free with Windows) on a regular basis (see Figure 3). It's not the most capable graphics editing program and I wouldn't use it to create more professional looking artwork such as book covers, but it's great for adding text labels to images and other quick notes.
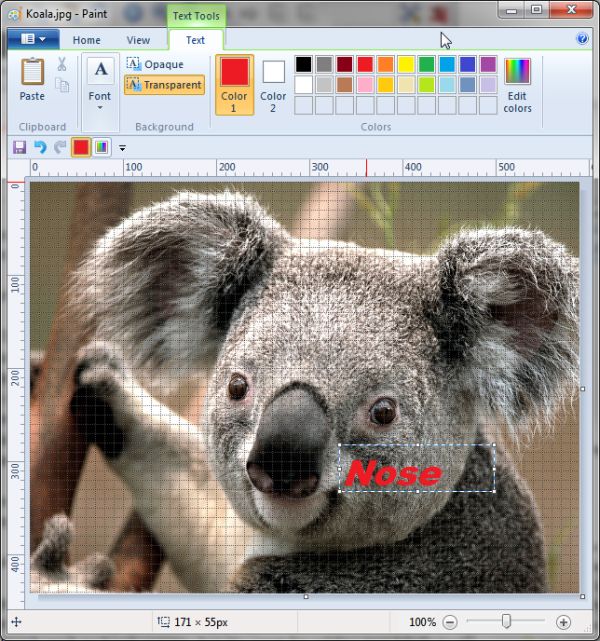
Figure 3. Windows Paint is great for quick jobs such as adding text labels or notes.
For processing photos before sending them off to Costco for printing, I use the editing feature in Windows Photo Gallery. It has all the basics for the amateur touchup, such as, red eye removal, color and exposure adjustment, and the latest version even has a retouch mode for removing blemishes. (Try removing someone's nose with retouch. It makes them look like Lord Voldemort from Harry Potter.)
For other more complex work such as book and magazine covers, I need more than either IrfanView or Windows Paint can offer.
Paint.Net for More Power
I've tried other free graphic programs such as GIMP, but Paint.Net was the easiest to learn and use for the available power and features (see Figure 4). I use it for creating covers for ComputorEdge and the e-books.
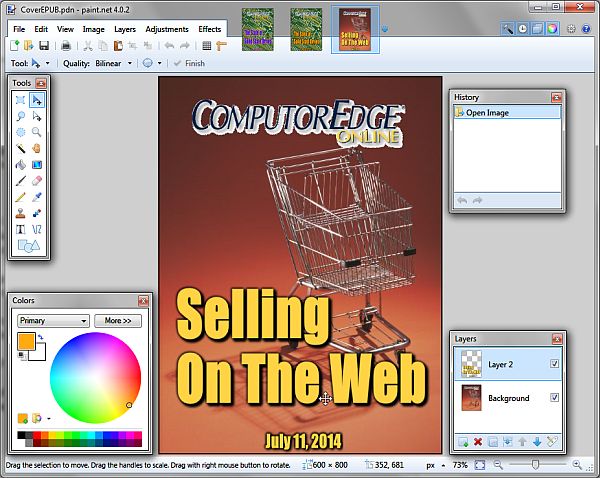
Figure 4. Paint.Net is one of the simpler free graphics layout and editing programs available. It can give a professional look to any artwork.
I will generally use IrfanView and Paint to preprocess images used in the covers, but when putting it all together I use Paint.Net. One of its best features is the use of layers for placing images and text on top of each other.
OpenOffice/LibreOffice
I do most of my writing directly on the Web in the software I wrote for ComputorEdge and the e-books. You could say that I was doing Cloud computing before I knew it was Cloud computing. All the programs run on a Web server and are accessible by anyone with the proper credentials and passwords. That means the apps are available through most browsers, but I find they work best in Google Chrome. Over the years I've noticed that Google has added pretty good spelling and grammar checking to the text editing boxes in Chrome. (I need all the help I can get.)
I could do my writing in the word processing package from Apache OpenOffice or LibreOffice (I have both), then cut and paste into the Web, but I find it easier to just write (and format) directly on the Web page. It's a simple process with very little formatting needed. For this reason, I rarely use the word processing in OpenOffice/LibreOffice. However, if I need to write a letter or quickly produce a document for printing, I do use one of these programs.
For example, I wanted to quickly print some pictures to enclose with a birthday card. I used OpenOffice Writer to insert some images and add captions (see Figure 5). I could have done this with other programs such as Paint.Net or even Windows Paint, but this was quick and easy to do while being oriented toward the printed page.
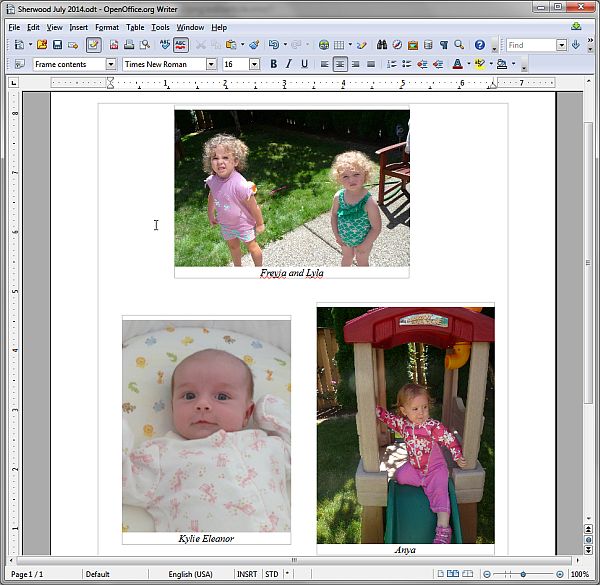
Figure 5. While any amount of writing can be done in OpenOffice Writer, the fact that it is text and printed page oriented makes it particularly useful for short quick jobs.
Both OpenOffice and LibreOffice include word processing, spreadsheets, presentations, graphics, and database software. I regularly use the spreadsheet package (Calc), but have had little reason to use the other programs. But, if you're looking for a free replacement for Microsoft Office (which won't overhaul the user interface every other year), then you may want to consider either (or both) of these packages. (OpenOffice and LibreOffice have grown from the same roots, although there may be a little divergence in the last few years. Yet, they use the same file formats and should be 99% compatible. For more information about the how the packages work see this OpenOffice/LibreOffice overview or the e-book Getting Started with OpenOffice (LibreOffice).)
(I just noticed that Digital Dave is giving the edge to LibreOffice.)
Notepad++ for Programming
I use Windows Notepad a lot. It's quick and easy when all I want is a text editor. I don't need to worry about formatting because, other than turning wordwrap on and off, there's none. Most of my short AutoHotkey scripts are written with Notepad. If I want a white background for a screen capture, I open Notepad and maximize the window. Notepad is the hammer and nail of text editing.
But if I'm doing more complex programming, such as that for the Web site and/or the e-book publishing program, then I turn to the free Notepad++ (see Figure 6). I can align program modules side-by-side moving code back and forth. I can open a number of snippet tabs simultaneously in the same window.
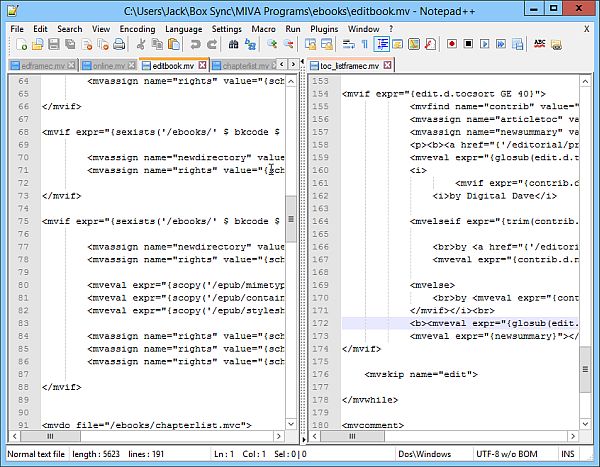
Figure 6. Notepad++ is designed for programmers offering many features that make coding easier.
Foxit PDF Reader
Foxit PDF Reader is such a good replacement for Adobe Reader that I recommend anyone still using Adobe Reader uninstall it completely and add Foxit to their Windows systems. While both programs are free, when compared to Foxit, Adobe Reader is a pig.
Why Not Adobe Reader?
Adobe invented the PDF (Portable Document Format) and Adobe Reader has been the king of the free PDF file reading software for decades (not unlike what Internet Explorer was in Web browsers). However, the software became more and more bloated over years, slowing down computers and annoying people with constant updates. All that most people really need was a light, fast PDF reader which doesn't hog memory.
It doesn't take much searching to find numerous comments about Adobe Reader such as, "Constant and bothersome updates plus huge footprint make Adobe Reader my least favorite PDF tool," and "Resource hog, unstable, bloated and highly insecure."
Both Google Chrome and Mozilla Firefox have their own light PDF reader built into their browser which has eliminated much of the need for Adobe Reader. However, there are times when you want to do more with a PDF file, plus it's nice to have a program not depended upon loading a Web browser. This is where Foxit PDF Reader comes in.
Why Foxit PDF Reader?
There are many free PDF readers available, but few of them have received the recognition of Foxit PDF Reader for its speed and capabilities. In addition to reading PDFs, Foxit allows the user to add comments directly to the PDF, fill in forms, and even has a limited feature for creating new PDFs from files, a scanner, or the Windows Clipboard.
The interface is intuitive with a ribbon toolbar system, but if you hate ribbon menus, you can set Foxit to the Classic Toolbar dropdown menu mode. One of the most notable features of Foxit is its ability to read PDFs out loud to the visually impaired and very young children.
E-Book Publishing
I'm sure that everyone has specialized programs they use which would not be for general consumption. To some degree the graphics programs I use fall into that category since most people may have no reason to take screenshots, manipulate them and put them into a Web site. Since I produce e-books on a regular basis, I also use Sigil EPUB Editor and Calibre E-Book Management for converting e-books into various formats. If you don't use or produce e-books, you may have no interest in these free programs.
We use Skype to see the grandkids who are out of town. But that has dropped off a little since the kids quickly get bored and start acting up with each other. It can be dizzying to watch children flying around the room.
Many Little AutoHotkey Apps
I have a ton of little AutoHotkey apps that automatically load every time I boot up. Over the last few years my feeling that AutoHotkey is absolutely the best free Windows utility software ever has only been reinforced. It can be remarkably simple to use or a script can get quite complex, but I believe that every Windows user, no matter their level (novice or advanced), has many reasons to want AutoHotkey—they just may not know it yet.
I use enough of these little apps that I had to make an AutoHotkey pop-up to list most of them as a reminder (see Figure 7). These scripts are tailored to my needs, but that's the point. AutoHotkey will make your Windows computer truly your computer.

Figure 7. A list of some of Jack's AutoHotkey features automatically loaded on boot up.
I have a number of other short AutoHotkey scripts which don't appear on the list because no reminder is necessary. For example, I use the AutoCorrect script for the most commonly misspelled words and special characters, such as the ¢ and £, which don't appear on the keyboard. These are hotstring replacements that correct errors the instant I misspell one of the words. I can't tell you how many times AutoCorrect has helped me, plus there's no need to remember hotkey combinations.
Am I trying to push everyone to use AutoHotkey? You bet! It is not a replacement for all the other free programs that I use regularly, but AutoHotkey can even make those free programs easier to operate. The only downside it that AutoHotkey does require a little script writing. But learning to write a little bit of code will make your brain nimble by stimulating new neural connections and expand your employment possibilities. (Want a taste of AutoHotkey? See our Introduction to AutoHotkey!) AutoHotkey is good for you and learning to write simple scripts will make your Windows life easier and help you lose weight. (Not kidding! See the CalorieCount app at the following links.) I have a bunch of free AutoHotkey apps posted at the ComputorEdge AutoHotkey download site. The apps are listed and descripted at the "Free AutoHotkey Scripts and Apps" Web page.
Free Software for Every Purpose
I've only listed the free programs which are important to me, but it is a pretty diverse group. Free software can certainly make life easier. If I were to pick one single program which adds more utililty for the Windows user than any other, I would be force to select AutoHotkey. If you use no other free Windows software, you should use AutoHotkey.
Why Use AutoHotkey?
Many programs such as Microsoft Word has features similar to those offered by AutoHotkey. You can do text replacement with a set of commonly misspelled words plus create macros (hotkeys) for quickly executing regular tasks. However, those tools in Microsoft Word only work in Word and a couple of other Microsoft products. AutoHotkey works everywhere you use it whether in a Windows program or on the Web. It even works in Word. AutoHotkey gives you an universality that you won't see in most Windows utilities.
AutoHotkey is easy to set up and use. It has tremendous flexibility. There is a long list of AutoHotkey commands which can be use for everything from sizing and moving windows to adding calendar events to your Windows computers. But you don't need to use any of these commands to get great benefit from AutoHotkey.
AutoHotkey is free and there are many free apps available for AutoHotkey .
AutoHotkey is Open Source which means no one person or company owns it. There are no license fees and you are free to use your scripts anywhere you like. There are very dedicated individuals who maintain, update and support AutoHotkey. They can be found by visiting the AutoHotkey Forums.
If you are concerned about how safe AutoHotkey is, see this AutoHotkey Forum topic.
For More Information
If you're interested in testing AutoHotkey to see if it might be right for you, then go to "Installing AutoHotkey and Writing Your First Script." This page shows you how to get up and running with AutoHotkey, plus it offers links to other articles on how to use AutoHotkey.
To see more of the many possible applications for AutoHotkey check out "Free AutoHotkey Scripts and Apps for Learning."
If you want more information in either the Amazon Kindle format, EPUB format for use on the iPad and other types of tablet computers (or on your PC), or PDF for printing on notebook size paper, then check out the following e-books by Jack Dunning:
Get this e-book, AutoHotkey Tricks You Ought to Do with Windows!
Now available in e-book format, Jack's A Beginner's Guide to AutoHotkey, Absolutely the Best Free Windows Utility Software Ever!: Create Power Tools for Windows XP, Windows Vista, Windows 7 and Windows 8.
Building Power Tools for Windows XP, Windows Vista, Windows 7 and Windows 8, AutoHotkey is the most powerful, flexible, free Windows utility software available. Anyone can instantly add more of the functions that they want in all of their Windows programs, whether installed on their computer or while working on the Web. AutoHotkey has a universality not found in any other Windows utility—free or paid.
Now in its second edition (October 2013), Jack takes you through his learning experience as he explores writing simple AutoHotkey scripts for adding repetitive text in any program or on the Web, running programs with special hotkeys or gadgets, manipulating the size and screen location of windows, making any window always-on-top, copying and moving files, and much more. Each chapter builds on the previous chapters. (The second edition now includes a chapter index of the AutoHotkey commands used in the book, plus Internet links directly to each commmand to the official AutoHotkey Web site.)
Also available at Amazon.com for the Kindle and Kindle software.
Jack's second AutoHotkey book which is comprised of updated, reorganized and indexed chapters from many of his sample applications is now available at ComputorEdge E-Books users. The book is organized and broken up into parts by topic. The book is not for the complete beginner since it builds on the information in A Beginner's Guide to AutoHotkey. However, if a person is reasonably computer literate, they could go directly to this book for ideas and techniques without the first book.
Jack shows how to build real world AutoHotkey applications. The AutoHotkey commands used are included in a special index to the chapters in which they appear. Even I can't remember everything I wrote."
Also available at Amazon.com for the Kindle and Kindle software.
To get more detailed information about AutoHotkey and see a List of AutoHotkey commands visit the AutoHotkey Web site.

